Pytorch中的 torch.distributions库详解

Pytorch torch.distributions库

Pytorch torch.distributions库

包介绍

torch.distributions包包含可参数化的概率分布和采样函数。 这允许构建用于优化的随机计算图和随机梯度估计器。

不可能通过随机样本直接反向传播。 但是，有两种主要方法可以创建可以反向传播的代理函数。

这些是

评分函数估计量 score function estimato
似然比估计量 likelihood ratio estimator
REINFORCE
路径导数估计量 pathwise derivative estimator
REINFORCE 通常被视为强化学习中策略梯度方法的基础，

路径导数估计器常见于变分自编码器的重新参数化技巧中。

虽然评分函数只需要样本 f(x)的值，但路径导数需要导数 f'(x)。

本文重点讲解Pytorch中的 torch.distributions库。

pytorch 的 torch.distributions 中可以定义正态分布：

import torch
from torch.distributions import  Normal
mean=torch.Tensor([0,2])
normal=Normal(mean,1)

sample()就是直接在定义的正太分布（均值为mean，标准差std是１）上采样：

result = normal.sample()
print("sample():",result)

输出：

sample(): tensor([-1.3362,  3.1730])

rsample()不是在定义的正太分布上采样，而是先对标准正太分布 N(0,1) 进行采样，然后输出： mean + std × 采样值

result = normal.rsample()
print("rsample():",result)

输出：

rsample: tensor([ 0.0530,  2.8396])

log_prob(value) 是计算value在定义的正态分布（mean,1）中对应的概率的对数，正太分布概率密度函数是:

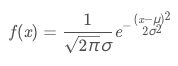
对其取对数可得:

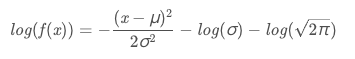
这里我们通过对数概率还原其对应的真实概率：

print("result log_prob:",normal.log_prob(result).exp())

输出：

result log_prob: tensor([ 0.1634,  0.2005])

到此这篇关于Pytorch中的 torch.distributions库的文章就介绍到这了,更多相关Pytorch torch.distributions库内容请搜索码农之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持码农之家！